µP

microPublication Biology

Sreedevi Padmanabhan1, Kaustuv Sanyal2§, and Dharanidhar Dubey1§

1Molecular Biology Laboratory, Veer Bahadur Singh Purvanchal University, Jaunpur- 222003, Uttar Pradesh, India.

2Molecular Mycology Laboratory, Molecular Biology and Genetics Unit, JNCASR, Bangalore - 560064, India.

§Correspondence to: Kaustuv Sanyal (sanyal@jncasr.ac.in) Dharanidhar Dubey (dddubey2003@gmail.com)

Abstract

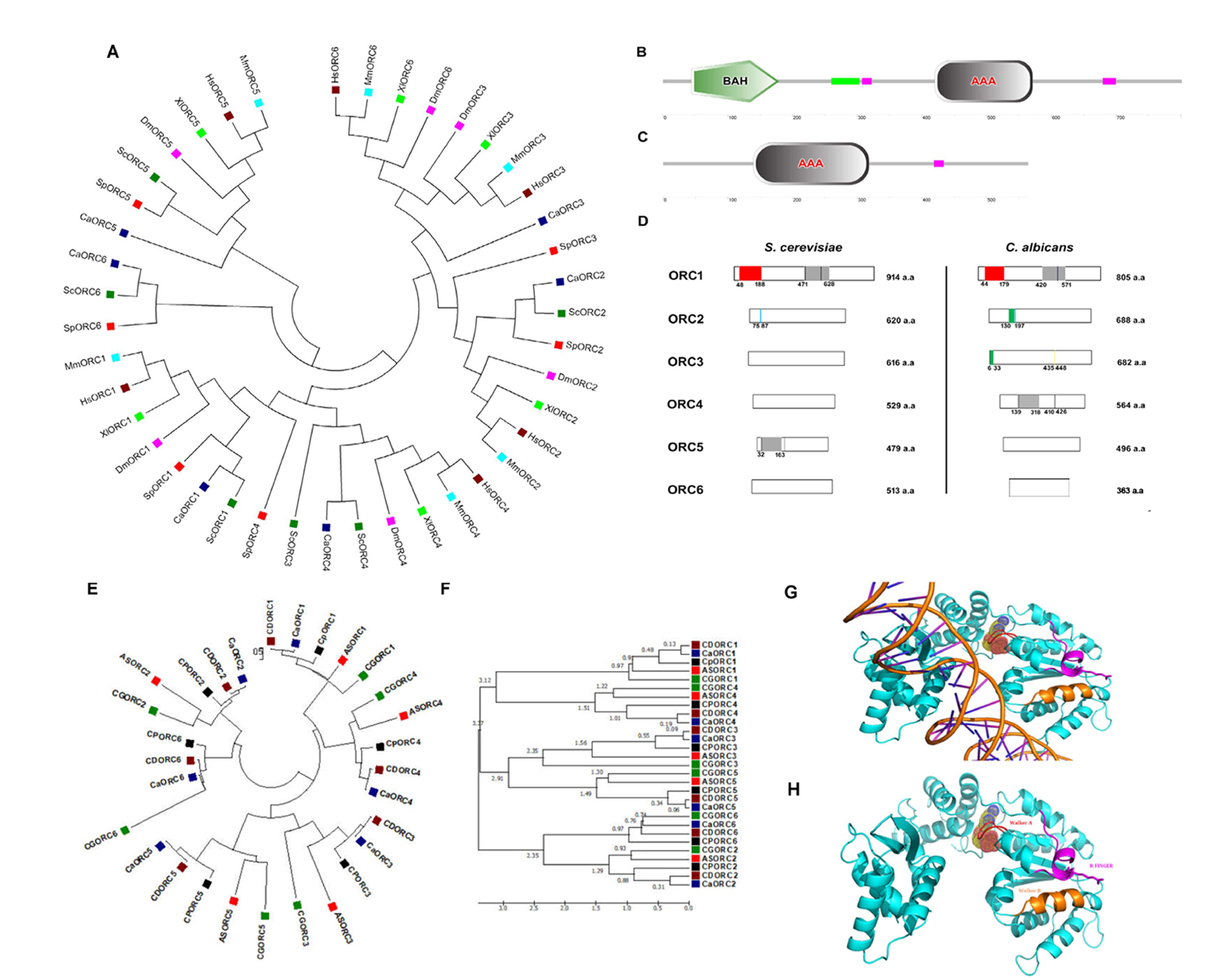
Description

Methods

Extended Data

  • Description: Extended data Figure1. Resource Type: Image. DOI: 10.22002/D1.2112
  • Description: Extended data Figure2. Resource Type: Image. DOI: 10.22002/D1.2113
  • Description: Extended Data Tables . Resource Type: Dataset. DOI: 10.22002/D1.2114
  • Description: Extended table dataset. Resource Type: Dataset. DOI: 10.22002/D1.2115

Acknowledgements

Funding

Author Contributions

  • Sreedevi Padmanabhan: Conceptualization, Formal analysis, Investigation, Software, Validation, Writing - original draft, Writing - review and editing, Data curation, Methodology
  • Kaustuv Sanyal: Conceptualization, Project administration, Supervision, Writing - review and editing, Resources, Funding acquisition, Formal analysis
  • Dharanidhar Dubey: Conceptualization, Funding acquisition, Project administration, Resources, Formal analysis, Supervision, Writing - review and editing

Reviewed By

Anonymous

History

  • Received: 2/22/2021
  • Revision Received: 9/8/2021
  • Accepted: 9/8/2021
  • Published: 9/21/2021

References

  1. PubMed
  2. PubMed
  3. PubMed
  4. PubMed
  5. PubMed
  6. PubMed
  7. PubMed
  8. PubMed
  9. PubMed
  10. PubMed
  11. PubMed
  12. PubMed
  13. PubMed
  14. PubMed
  15. PubMed
  16. PubMed
  17. PubMed
  18. PubMed
  19. PubMed
  20. PubMed
  21. PubMed
  22. PubMed
  23. PubMed
  24. PubMed
  25. 10.1021/ci960402j.
  26. PubMed
  27. PubMed
  28. PubMed
  29. PubMed
  30. PubMed
  31. PubMed
  32. PubMed
  33. PubMed

Copyright

© 2021 by the authors. This is an open-access article distributed under the terms of the Creative Commons Attribution 4.0 International (CC BY 4.0) License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Citation

PubMed Central: PMC8456302

PubMed: 34568775

Cited By

Article in Genome Research, published January 2021

microPublication Biology is published by

1200 E. California Blvd. MC 1-43 Pasadena, CA 91125

The microPublication project is supported by

The National Institute of Health -- Grant #: 1U01LM012672-01

microPublication Biology:ISSN: 2578-9430